Math behind Piano keys
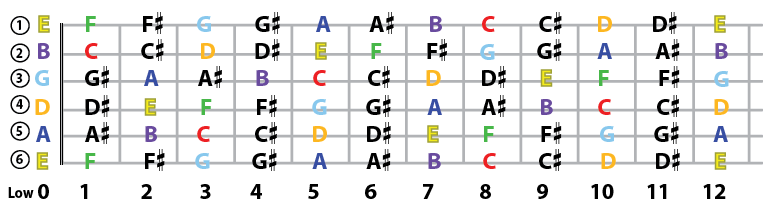
Relationship between key groups
- piano keys are made of a set of octave key groups, each octave key group made from 7 white keys and 5 in-between black keys. (total 12 keys per octave key group)
- each octave key group is double the sound frequency of previous octave key groups
- example,
- octave key group 1, containing 7 white keys {“C1”,“D1”,“E1”,“F1”,“G1”,“A1”,“B1”}, its “C1” key is at sound frequency of 32.703Hz; plus 5 black keys means {“C”,“d_b”,“D”,“e_b”,“E”,“F”,“g_b”,“G”,“a_b”,“A”,“b_b”,“B”};
- the C2 key from octave key group 2 is at sound frequency of 65.406 HZ, that is 32.703×2.
- the middle group (4th group), C4 is at 261.6Hz, = 65.406*2^2
- as you can see, the number is exact “times power of 2”, as you can guess, C7=C1x[2^(7-1)] =32.703×64=2092.9 (about 2093Hz)
- youtube:
- Music and math: The genius of Beethoven - Natalya St. Clair
- beats and math
Frequency Relationship within a key group and White vs Black keys
- study 1st octave key group, white keys {“C1”,“D1”,“E1”,“F1”,“G1”,“A1”,“B1”}
- C1=32.703Hz
- D1=36.708Hz = C1 + 4.0Hz
- E1=41.203Hz = D1 + 4.5Hz
- F1=43.654Hz = E1 + 2.4Hz (so F1 is “half step”, aka “half incremental” from E1)
- G1=48.999HZ = F1 + 5.3Hz
- A1=55.000Hz = G1 + 6.0Hz
- B1=61.735Hz = A1 + 6.7Hz
- C2=65.406Hz = B1 + 3.7Hz (so C2 is mostly like “half step” from B1)
- so we can see, the incremental is based of a power function curve.
- based on that, “half step” incremental white keys has no in-between black keys, while those “full” incremental white keys has in-between black keys, representing the “half-step” frequency increase.
- in short, all keys in piano are layout in “half step” increment, either “black to white”, or “white to black”, or “white to white” is a “half step”.
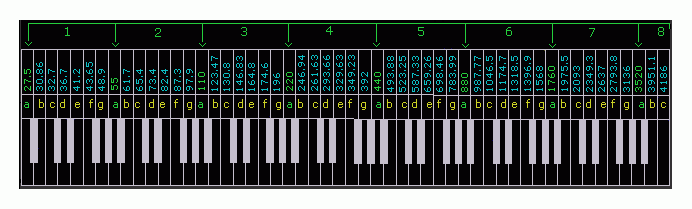
How Many key groups we need
- while average human can hear from 20Hz to 8000Hz, so from C1 32.7Hz to C8 4186Hz reaching C9's 8392Hz are enough;
- which means 8 sets * (7 white key+ 5 black key) = 96 keys
How much frequency difference to make a key identifiable and photographic-like-color-depth
- as in previous calculation, the lower the frequency, the lower the frequency difference between keys, like C1 and D1 are just 4Hz apart, C4 and D4 are 32Hz+ apart. (4Hz x2^3= 32Hz)
- however, the real human hearing factor is that the effect of each key difference is about similar, like “count extra 4 hits from 32 hits in 1 second” has similar effect of count “extra 400 hits from 3200 hits in 1 second”;
- it is more a ratio difference than a count difference
- compare D1 to C1 (full step), 4Hz difference is roughly 1/8 of 32.703Hz (C1); D1=C1 * 1.12;
- compare B1 to A1 (full step), 6.7Hz difference is roughly 1/8 of 55Hz (A1); B1=A1 * 1.12;
- compare F1 to E1 (half step), 2.4Hz difference is roughly 1/16 of 41.203Hz (E1); F1=E1 * 1.06;
- compare C2 to B1 (half step), 3.7Hz difference is roughly 1/16 of 61.735Hz (B1); C2=B1 * 1.06;
- so,
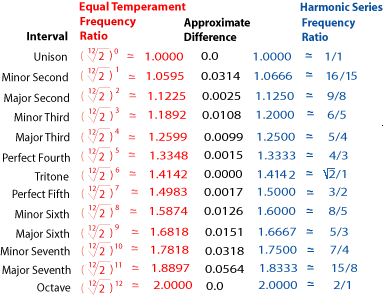
- each key of piano is half step from nearby one, that is 1.06 times higher or lower than nearby one.
- each “full step” is 1.12 times higher or lower; since 1.12 = 1.06 * 1.06;
- each octave is 12 keys (half step) difference, power(1.06, 12) = 2
- more accurately wrriten as power(1.0595, 12) = 2
- so to pianist term, roughly 1/16 difference (or accurately 0.0595 difference) is about the minimum frequency difference to make identifiable
- related read:
- “Equations for the Frequency Table” http://www.phy.mtu.edu/~suits/NoteFreqCalcs.html
- Note names and frequencies calculator: http://www.sengpielaudio.com/calculator-notenames.htm
Frequency and Loudness
- we often find, low frequency keys like in C1-C3 range, need to press harder than normal to make them sounds loud; while C4-C5 are easy to make it loud; while C6 and higher sound are easier to think it loud. that is because our hearing are sensitive to high frequency sound.
- here is a graph of “how loud” is same “loudness” for different frequency, based on our human ear “thinks”: http://en.wikipedia.org/wiki/Equal-loudness_contour
- Absolute threshold of hearing: http://en.wikipedia.org/wiki/Absolute_threshold_of_hearing
- and our human ear use “Phon” as loudness measurement unit, while “dB (sound pressure)” is scentific measurement unit.
All musical notation related images
Property of Sound - soundwave and wave in general
- wave has these property (think of those waterwave)
- amplitude: height of wave
- wave length: distance between 2 high points
- period/frequency: circle time, or circle per second
- speed = wave length * frequency: how fast high point shift away
- soundwave
- amplitude: aka “volume, sound pressure”
- wave length:
- frequency: aka “pitch”, range from 10Hz to 1000kHz,
- (Human range from 20Hz to 10kHz, piano 20Hz to 8kHz)
- speed: in air, about 300m/s; thus also means high frequency sound has short wavelength.
- lightwave
- frequency: around 10^14Hz, (100THz)
- sound to humans
- low frequency sound travels further, because of lower frequency are less absorbed when traveling through medium, and also less reflected by medium (better penetration into another medium)
- high frequency are more noticeable to humans, due to human ear nature.
- sound “loudness” to human are affected by amplitude, frequency, bandwidth and duration.
Training Learning in keyboards
- Jingle All the way: http://www.youtube.com/watch?v=wC62sFbfuvE
- We Wish You a Merry Christmas (Christmas Carol) [Easy Piano Tutorial] http://www.youtube.com/watch?v=8yYzd985jL8
- Silent Night (Christmas Carol) [Easy Piano Tutorial] http://www.youtube.com/watch?v=MVlQkgw7OBM
- Jingle Bells (Christmas Carol) [Easy Piano Tutorial] http://www.youtube.com/watch?v=rvGOgEByv0o
- Twinkle, Twinkle, Little Star [Easy Piano Tutorial] http://www.youtube.com/watch?v=HbUbYE9zQ6k
- Mozart version : http://www.youtube.com/watch?v=KKCsujeeu8o
- Guitar version : http://www.youtube.com/watch?v=E5xr_JPGNeA
- Happy Birthday to You [Easy Piano Tutorial] http://www.youtube.com/watch?v=RZIy9UdWi7E
Songs
- Japanese song
Some tutorial collection
Reference Site
Reference Book
- Piano Adventures series by Nancy and Randall Faber
- John Thompson's easiest piano course
- John Thompson's Modern course for the piano
- Hanon 60 exercises
- Czerny op. 599
- Aural Training in Practise book 1 by Ronald Smith
ref: https://www.kiasuparents.com/kiasu/forum/viewtopic.php?f=12&t=47244
3D visualization
- Maya code on generating piano keys
- white key on even X axis spacing, and Y axis represent half step and whole step relationship
- here is mel code
string $names[]={"C","D","E","F","G","A","B"}; string $names2[]={"C","d_b","D","e_b","E","F","g_b","G","a_b","A","b_b","B"}; // -- white keys only $total=7*5; for ($i=0;$i<$total;$i++){ int $n=$i%7; int $oct=$i/7; $tCube=`polyCube -ch on -o on -w 1 -h 1 -d 2 -cuv 4 -n ($names[$n]+"_1")`; float $s=$n; if($n>=3) $s=$s-0.5; move -a $i ($oct*6+$s) $oct $tCube[0]; } for($i=1;$i<=5;$i++){ select -r ("*_"+$i); group -n ("octGrp_"+$i); } // -- white keys and black keys $total=12*5; for ($i=0;$i<$total;$i++){ int $n=$i%12; int $oct=$i/12; $tCube=`polyCube -ch on -o on -w 1 -h 1 -d 2 -cuv 4 -n ("ns1:"+$names2[$n]+"_1")`; string $sn=$tCube[0]; move -a ($oct*6+$n*0.5+$oct) ($oct*6+$n*0.5) ($oct+10) $tCube[0]; if($n>=5) move -r 0.5 0 0 $tCube[0]; if(`gmatch $sn "*_b_*"`) move -r 0 0 -.5 $tCube[0]; }